Twierdzenie Bayesa: poznaj jeden z filarów rachunku prawdopodobieństwa!
Twierdzenie Bayesa jest jednym z filarów prawdopodobieństwa. Nazwa tego twierdzenia pochodzi od Thomasa Bayesa (1702 – 1761), który zaproponował tę teorię w XVIII wieku. Ale co dokładnie Bayes próbował wyjaśnić?
Według słownika Meriam-Webster prawdopodobieństwo jest „stosunkiem liczby wyników w wyczerpującym zestawie równie prawdopodobnych wyników, które dają dane zdarzenie do całkowitej liczby możliwych wyników”.
Wiele teorii prawdopodobieństwa rządzi światem. Na przykład, kiedy idziesz do lekarza on przepisuje Ci to co najprawdopodobniej Cię wyleczy. Ponadto reklamodawcy koncentrują swoje kampanie na ludziach, którzy chętniej kupują promowany przez nich produkt. Ponadto wybierasz codzienne dojazdy na trasie, która z większym prawdopodobieństwem zajmie Ci mniej czasu. Jak więc używać twierdzenie Bayesa?
Twierdzenie Bayesa – najpierw poznajmy twierdzenie o prawdopodobieństwie całkowitym
Jednym z najbardziej znanych praw prawdopodobieństwa jest twierdzenie o prawdopodobieństwie całkowitym. Ważne jest, aby przeanalizować jakie jest to twierdzenie o prawdopodobieństwie całkowitym. Aby to zrozumieć podamy przykład.
Powiedzmy, że w przypadkowym kraju 39% obywateli to kobiety. Wiemy również, że 22% kobiet i 14% mężczyzn nie ma pracy. Jakie jest zatem prawdopodobieństwo P, że osoba wybrana losowo z populacji aktywnej w tym kraju jest bezrobotna P (U)?

Zgodnie z teorią prawdopodobieństwa, wyrażamy je w ten sposób:
- Prawdopodobieństwo, że dana osoba była kobietą: P (W)
- Prawdopodobieństwo, że dana osoba była mężczyzną: P (M)
Ponieważ wiemy, że 39% obywateli to kobiety, możemy wywnioskować, że P (W) = 0,39
Możemy zatem wnioskować, że P (M) = 1 – 0,39 = 0,61.
Podany problem daje nam także prawdopodobieństwa warunkowe:
- Prawdopodobieństwo, że kobieta jest bezrobotna: P (U | W) = 0,22
- Prawdopodobieństwo, że mężczyzna jest bezrobotny: P (U | M) = 0,14
Dlatego też, stosując prawo całkowitego prawdopodobieństwa, otrzymujemy:
P (U) = P (W) × P (U | W) + P (M) × P (U | M)
Czyli P (U) = 0,22 × 0,39 + 0,14 × 0,61
A zatem P (U) = 0,17
Zatem prawdopodobieństwo, że wybrana losowo osoba nie będzie miała pracy P (U) wyniesie 0,17. Widać, że wynik leży między dwoma prawdopodobieństwami warunkowymi (0,14 <0,17 <0,22).
Właściwe twierdzenie Bayesa
Przypuśćmy teraz, że wybrałeś przypadkową osobę dorosłą do wypełnienia formularza i zdałeś sobie sprawę, że nie mają pracy. W tym przypadku biorąc pod uwagę poprzedni przykład, jakie jest prawdopodobieństwo, że osoba którą wybrałeś przypadkowo jest kobietą [P (W | U)]?
Aby rozwiązać ten problem, musisz zastosować twierdzenie Bayesa. W szczególności używamy tego twierdzenia do obliczenia prawdopodobieństwa zdarzenia, biorąc pod uwagę poprzednie informacje o tym wydarzeniu. Możesz obliczyć prawdopodobieństwo zdarzenia A wiedząc również, że to zdarzenie A spełnia pewne cechy (B), które wpływają na jego prawdopodobieństwo.
W tym przypadku mówimy o prawdopodobieństwie, że osoba którą wybrałeś losowo do wypełnienia formularza to kobieta. Ponadto prawdopodobieństwo nie będzie niezależne od tego czy dana osoba ma pracę czy nie.
Wzór twierdzenia Bayesa
Jak każde inne twierdzenie, potrzebujemy formuły do obliczenia prawdopodobieństwa:
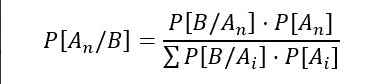
Chociaż wydaje się to trudne, wszystko ma wyjaśnienie:
- Na początek, B jest wydarzeniem, o którym wcześniej przeczytaliśmy.
- Z drugiej strony, termin A (n) odnosi się do różnych zdarzeń warunkowych.
- W liczniku mamy prawdopodobieństwo warunkowe. Odnosi się to do prawdopodobieństwa, że coś (zdarzenie A) wystąpi wiedząc, że występuje również inne zdarzenie (B). Definiujemy to jako P (A | B) i wyrażamy to jako „prawdopodobieństwo A przy danym B”.
- W mianowniku mamy odpowiednik P (B).

Przykład
Wracając do poprzedniego przykładu załóżmy, że wybrałeś przypadkową osobę dorosłą do wypełnienia kwestionariusza i zdałeś sobie sprawę, że ta nie ma pracy. Jakie jest prawdopodobieństwo, że ta osoba jest kobietą [P (W | U)]?
Cóż, biorąc pod uwagę poprzedni przykład wiemy, że 39% aktywnej populacji stanowią kobiety. Wiemy wtedy, że reszta to mężczyźni. Ponadto wiemy, że odsetek bezrobotnych kobiet wynosi 22%, a odsetek bezrobotnych mężczyzn wynosi 14%.
Wreszcie wiemy, że prawdopodobieństwo wyboru losowej osoby bezrobotnej wynosi 0,17. Jeśli więc zastosujemy twierdzenie Bayesa, otrzymamy wynik w wysokości 0,5 prawdopodobieństwa, że wybrana losowo osoba spośród wszystkich bezrobotnych będzie kobietą.
P (W | U) = (P (W) * P (U | W) / P (U)) = (0,22 * 0,39) / 0,17 = 0,5
Zakończymy ten artykuł odwołując się do jednego z najczęstszych nieporozumień dotyczących prawdopodobieństwa. Może mieścić się w zakresie od 0 do 1. Jeśli prawdopodobieństwo zdarzenia wynosi 0 to znaczy, że jest ono niemożliwe, aby się wydarzyło. Z drugiej strony, jeśli prawdopodobieństwo wynosi 1, wtedy na pewno się wydarzy.
Twierdzenie Bayesa jest jednym z filarów prawdopodobieństwa. Nazwa tego twierdzenia pochodzi od Thomasa Bayesa (1702 – 1761), który zaproponował tę teorię w XVIII wieku. Ale co dokładnie Bayes próbował wyjaśnić?
Według słownika Meriam-Webster prawdopodobieństwo jest „stosunkiem liczby wyników w wyczerpującym zestawie równie prawdopodobnych wyników, które dają dane zdarzenie do całkowitej liczby możliwych wyników”.
Wiele teorii prawdopodobieństwa rządzi światem. Na przykład, kiedy idziesz do lekarza on przepisuje Ci to co najprawdopodobniej Cię wyleczy. Ponadto reklamodawcy koncentrują swoje kampanie na ludziach, którzy chętniej kupują promowany przez nich produkt. Ponadto wybierasz codzienne dojazdy na trasie, która z większym prawdopodobieństwem zajmie Ci mniej czasu. Jak więc używać twierdzenie Bayesa?
Twierdzenie Bayesa – najpierw poznajmy twierdzenie o prawdopodobieństwie całkowitym
Jednym z najbardziej znanych praw prawdopodobieństwa jest twierdzenie o prawdopodobieństwie całkowitym. Ważne jest, aby przeanalizować jakie jest to twierdzenie o prawdopodobieństwie całkowitym. Aby to zrozumieć podamy przykład.
Powiedzmy, że w przypadkowym kraju 39% obywateli to kobiety. Wiemy również, że 22% kobiet i 14% mężczyzn nie ma pracy. Jakie jest zatem prawdopodobieństwo P, że osoba wybrana losowo z populacji aktywnej w tym kraju jest bezrobotna P (U)?

Zgodnie z teorią prawdopodobieństwa, wyrażamy je w ten sposób:
- Prawdopodobieństwo, że dana osoba była kobietą: P (W)
- Prawdopodobieństwo, że dana osoba była mężczyzną: P (M)
Ponieważ wiemy, że 39% obywateli to kobiety, możemy wywnioskować, że P (W) = 0,39
Możemy zatem wnioskować, że P (M) = 1 – 0,39 = 0,61.
Podany problem daje nam także prawdopodobieństwa warunkowe:
- Prawdopodobieństwo, że kobieta jest bezrobotna: P (U | W) = 0,22
- Prawdopodobieństwo, że mężczyzna jest bezrobotny: P (U | M) = 0,14
Dlatego też, stosując prawo całkowitego prawdopodobieństwa, otrzymujemy:
P (U) = P (W) × P (U | W) + P (M) × P (U | M)
Czyli P (U) = 0,22 × 0,39 + 0,14 × 0,61
A zatem P (U) = 0,17
Zatem prawdopodobieństwo, że wybrana losowo osoba nie będzie miała pracy P (U) wyniesie 0,17. Widać, że wynik leży między dwoma prawdopodobieństwami warunkowymi (0,14 <0,17 <0,22).
Właściwe twierdzenie Bayesa
Przypuśćmy teraz, że wybrałeś przypadkową osobę dorosłą do wypełnienia formularza i zdałeś sobie sprawę, że nie mają pracy. W tym przypadku biorąc pod uwagę poprzedni przykład, jakie jest prawdopodobieństwo, że osoba którą wybrałeś przypadkowo jest kobietą [P (W | U)]?
Aby rozwiązać ten problem, musisz zastosować twierdzenie Bayesa. W szczególności używamy tego twierdzenia do obliczenia prawdopodobieństwa zdarzenia, biorąc pod uwagę poprzednie informacje o tym wydarzeniu. Możesz obliczyć prawdopodobieństwo zdarzenia A wiedząc również, że to zdarzenie A spełnia pewne cechy (B), które wpływają na jego prawdopodobieństwo.
W tym przypadku mówimy o prawdopodobieństwie, że osoba którą wybrałeś losowo do wypełnienia formularza to kobieta. Ponadto prawdopodobieństwo nie będzie niezależne od tego czy dana osoba ma pracę czy nie.
Wzór twierdzenia Bayesa
Jak każde inne twierdzenie, potrzebujemy formuły do obliczenia prawdopodobieństwa:
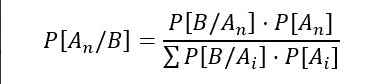
Chociaż wydaje się to trudne, wszystko ma wyjaśnienie:
- Na początek, B jest wydarzeniem, o którym wcześniej przeczytaliśmy.
- Z drugiej strony, termin A (n) odnosi się do różnych zdarzeń warunkowych.
- W liczniku mamy prawdopodobieństwo warunkowe. Odnosi się to do prawdopodobieństwa, że coś (zdarzenie A) wystąpi wiedząc, że występuje również inne zdarzenie (B). Definiujemy to jako P (A | B) i wyrażamy to jako „prawdopodobieństwo A przy danym B”.
- W mianowniku mamy odpowiednik P (B).

Przykład
Wracając do poprzedniego przykładu załóżmy, że wybrałeś przypadkową osobę dorosłą do wypełnienia kwestionariusza i zdałeś sobie sprawę, że ta nie ma pracy. Jakie jest prawdopodobieństwo, że ta osoba jest kobietą [P (W | U)]?
Cóż, biorąc pod uwagę poprzedni przykład wiemy, że 39% aktywnej populacji stanowią kobiety. Wiemy wtedy, że reszta to mężczyźni. Ponadto wiemy, że odsetek bezrobotnych kobiet wynosi 22%, a odsetek bezrobotnych mężczyzn wynosi 14%.
Wreszcie wiemy, że prawdopodobieństwo wyboru losowej osoby bezrobotnej wynosi 0,17. Jeśli więc zastosujemy twierdzenie Bayesa, otrzymamy wynik w wysokości 0,5 prawdopodobieństwa, że wybrana losowo osoba spośród wszystkich bezrobotnych będzie kobietą.
P (W | U) = (P (W) * P (U | W) / P (U)) = (0,22 * 0,39) / 0,17 = 0,5
Zakończymy ten artykuł odwołując się do jednego z najczęstszych nieporozumień dotyczących prawdopodobieństwa. Może mieścić się w zakresie od 0 do 1. Jeśli prawdopodobieństwo zdarzenia wynosi 0 to znaczy, że jest ono niemożliwe, aby się wydarzyło. Z drugiej strony, jeśli prawdopodobieństwo wynosi 1, wtedy na pewno się wydarzy.
Wszystkie cytowane źródła zostały gruntownie przeanalizowane przez nasz zespół w celu zapewnienia ich jakości, wiarygodności, aktualności i ważności. Bibliografia tego artykułu została uznana za wiarygodną i dokładną pod względem naukowym lub akademickim.
- 4. PROBABILIDAD CONDICIONADA Y EL TEOREMA DE BAYES. Retrieved from http://webcache.googleusercontent.com/search?q=cache:0EF2amyeIKMJ:halweb.uc3m.es/esp/Personal/personas/mwiper/docencia/Spanish/Teoria_Est_El/tema4_orig.pdf+&cd=13&hl=es&ct=clnk&gl=es&client=firefox-b-ab
- Díaz, C., & de la Fuente, I. (2006). Enseñanza del teorema de Bayes con apoyo tecnológico. Investigación en el aula de matemáticas. Estadística y Azar.
- Teorema de Bayes – Definición, qué es y concepto | Economipedia. Retrieved from https://economipedia.com/definiciones/teorema-de-bayes.html
Ten tekst jest oferowany wyłącznie w celach informacyjnych i nie zastępuje konsultacji z profesjonalistą. W przypadku wątpliwości skonsultuj się ze swoim specjalistą.







